在微观世界里，自旋和质量一样是所有微观粒子的基本属性。原子核的自旋来自于质子和中子，根据泡利不相容原理，原子核内成对的质子或中子的自旋相互抵消。因此，只有奇数质子或奇数中子的原子核才有净自旋。

图1：原子自旋核的自旋

具有净自旋的原子核，其自旋磁矩也不为零，被称为磁性核，它们都可以产生核磁共振现象。如最常见的有¹H，¹³C，¹⁹F，³¹P等，在量子力学中，原子核的自旋磁矩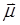与自旋角动量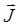之间存在如下关系：

                          （公式1）

其中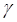是该原子核的旋磁比，不同原子核的旋磁比值都不同。

由于磁性核的自旋磁矩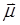不为零，所以它们在外磁场中，会受到一个磁力矩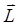的作用：

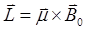                           （公式2）

根据角动量定理（牛顿第二定律的角动量形式），该力矩与自旋角动量之间的关系满足下式：

                        （公式3）

根据以上三个公式，联立可求得磁性核在外磁场中的运动方程为：

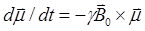               （公式4）

上式表示核磁矩在外磁场中的进动，称之为拉莫尔进动。由于核磁矩是一个恒模矢量，而恒模矢量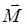的进动方程恰恰可用下式来表示，其中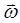是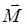进动的角频率：

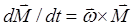                （公式5）

因此，结合公式（4）和公式（5），我们又可以得到核磁矩在外磁场中进动的角频率（又称为拉莫尔频率）：

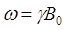               （公式6）    

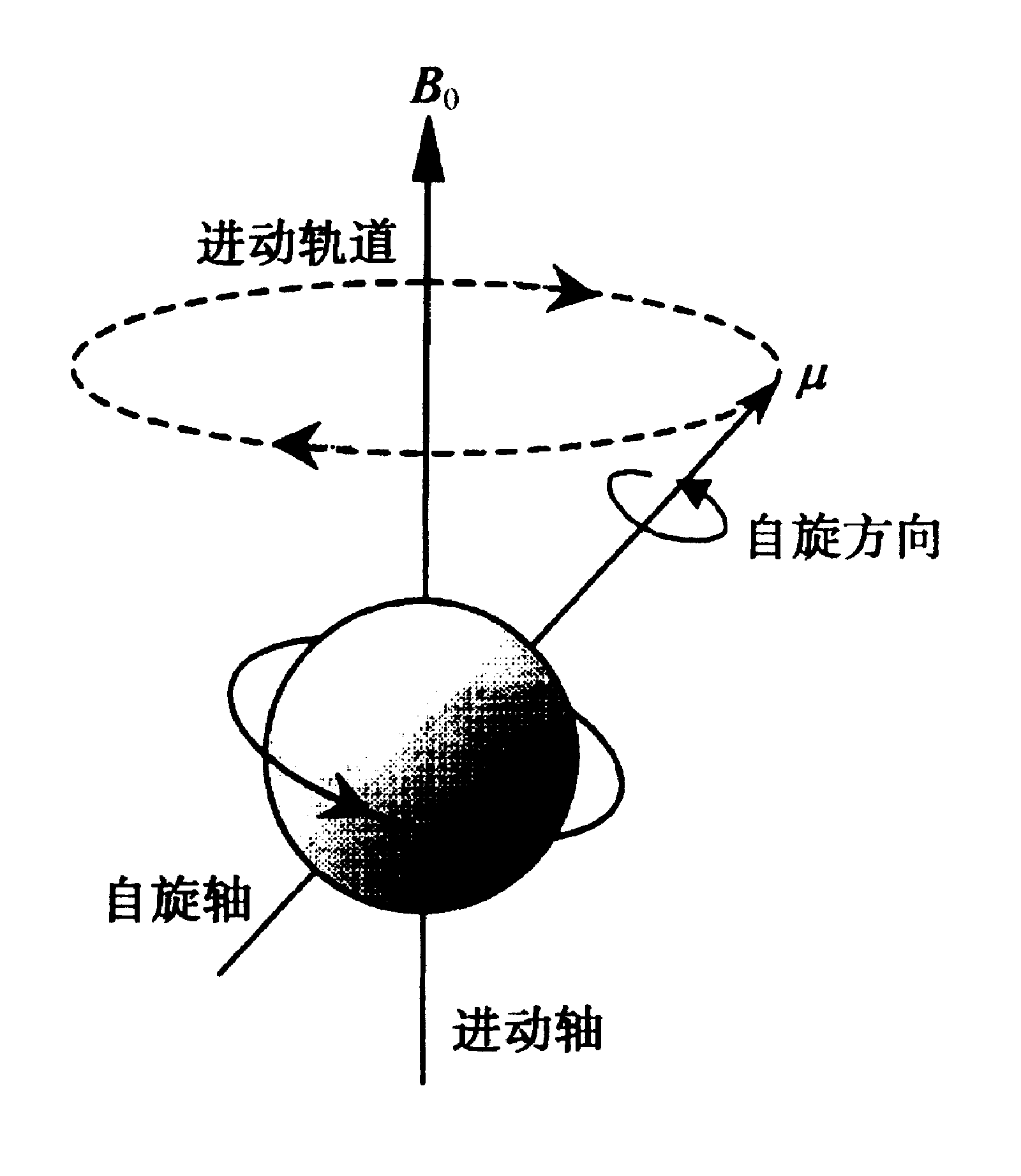
图2：核磁矩的进动示意图

原子核的自旋磁矩在无磁场的情况下，能级是简并的，对应杂乱无章的无序排列。当施加外磁场后，能级简并解除，能级发生分裂，对应磁矩的有序排列。有序排列的磁矩在进动时会按照与外磁场保持一定的夹角。

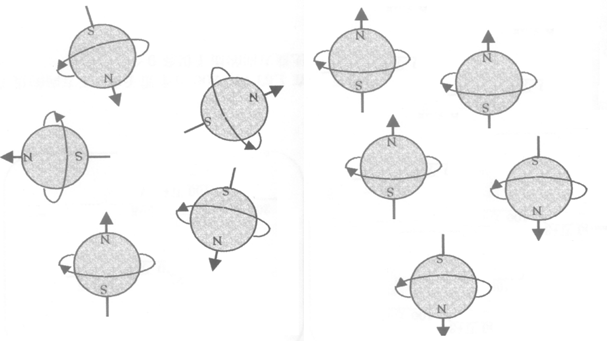
图3：磁矩的无序排列与有序排列

不同的自旋磁矩有序排列对应于原子核不同的进动夹角和进动方向，以最简单的氢原子核为例，自旋量子数为1/2，故能级只分为两个，两能级之间的能量差为：

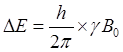                      （公式7）         

其中，h是普朗克常数。根据量子力学的跃迁理论，当存在频率为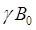的电磁波时，大量处于低能级的原子核就能吸收能量跃迁至高能级上。这就是核磁共振现象的基本原理。当然，不同能级之间的跃迁不仅需要满足能量守恒，还必须满足角动量守恒，因此只有垂直于静磁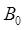场的射频场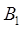才能发挥作用。

图4：核磁共振的原理示意图

综上所述，射频电磁波的频率应等于原子核的拉莫尔进动频率，这是发生核磁共振现象的必备条件之一！必备条件之二是射频场必须与静磁场正交，或者说只有正交射频场分量才能使原子核发生能级跃迁。